As Itility we are always interested in joining forces with young professionals. So we are glad with the opportunity to facilitate a workshop at the National Mathematical Symposium (NMS), themed Modern World Mathematics, organized at the Natlab in Eindhoven. 

The symposium was joined by students with various backgrounds (mathematics, economics, and many others) coming from across the Netherlands.

The day featured a series of lectures presenting examples of projects, where mathematics was employed to solve everyday problems, combined with the workshops where students could tackle a practical challenge.

The workshop

After a brief introduction of myself, Itility’s structure, and goals it was time to showcase some of the projects we carried out. I briefly mentioned two cases where we used math in real life: one was an optimized allocation of licenses, the other on optimizing the capacity of IT infrastructure; in both those cases we managed to reduce running costs and gain control over potential issues (as well as prevent user frustration).

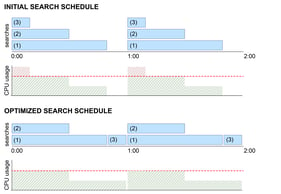
Next, I introduced the project where we optimized backup schedules. This was the basis for the case the students were going to work on: to develop a model that would optimize the use of the computer power and spread searches in time, in a way that would prevent overloading of the CPUs.

I mentioned two possible approaches to solve this problem – linear programming and simulated annealing. However, due to time constraints focused only on the linear programming.

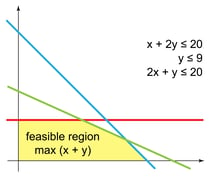
Linear programming is a method that was developed to achieve the best outcome (such as maximum profit or lowest cost), based on a mathematical model whose requirements are represented by linear relationships. It can be summarized by the following graphic where the feasible region represents the case where all of the model constraints are met.

The challenge

To illustrate how linear programming can be used in solving everyday problems I showed a simple example of optimizing profits. In this theoretical exercise you are given a backpack that can hold up to a 100 kg load and a selection of items of different values and weights. The task is to make a selection of items that you’d be able to carry in the backpack and will sell for the highest profit. To summarize it in the linear programming fashion the conditions are:

After presenting the theoretical background and a warm-up example it was time to give our participants a go at developing their own solutions with the provided data - a dataset containing searches with their specified offset times and lengths of each search’s run. The challenge was to come up with constraints in the form of the linear equations, re-write the R code provided for the “backpack task” and finally try to identify some of the potential problems that may occur while running their search schedules. And off they started!

An extra hint

After approximately 20 minutes of intensive work, it was time to take a short break to summarize the current progress and mention some of the issues that might have arisen. Interestingly, while most of the proposed solutions were correct from a theoretical perspective, they would take too much time to solve as they were too large or did not take into account practical constraints.

It was time for an extra clue for the team: solve the problem based on the principles of Dantzig-Wolfe decomposition.

Dantzig-Wolfe decomposition is an algorithm for solving linear programming problems. What the algorithm does is it generates so-called delayed columns each of which contains (in our case) a set of searches with delayed offset. By solving those independent sub-problems you can find the best fitting schedules. A practical modification of this method, which is also an easier approach to problem at hand, is to pick random schedules, and solve only the master problem.  

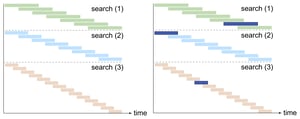
After sharing this clue, it was then only fair to also introduce some of the other challenges that may appear while developing the solution and that will have to be incorporated into their model:

• Different duration of the searches - the length of the search is influenced by the number of other searches running at the same time;
• Interdependency of the searches - some of searches can only be run if another search was run first;
• Night versus day time - most of the scheduled searches should be run outside of the office hours, to avoid frustrations of “day time users”;
• Robustness of the system - the model should be easily adjustable based on a day to day needs and small changes that may occur;

Having all those conditions the students were given another 20 minutes to work in groups.

The time passed fast and a few minutes before the end I revealed the final solution. Unfortunately, none of the teams managed to fully solve the problem, but given the time some of teams made a substantial progress in getting there and were rewarded with small prizes.

Are you interested in solving this challenge yourself? You can download it here.